Outpatient forecasting model in spine hospital using ARIMA and SARIMA methods
Introduction
Korea has recently experienced a trend of very rapidly progressing population aging. This trend has been accompanied by the growing role of specialized hospitals that treat geriatric illnesses (1). Specialized hospitals have evolved beyond their previous role of simply treating illnesses to that of providing preventive medical services, thus contributing to ensuring that more Koreans can lead healthy lives in this “centenarian age” (2).
However, since the 2000s, specialized hospitals have been met with challenges in management due to the rising number of major hospitals and the opening up of the medical sector. The growing number of medical institutions has presented patients with a broader choice of hospitals, while the increased accessibility of information via smartphones and the internet has combined with a higher level of awareness to allow patients to search for hospitals offering high-quality medical services by collecting information via various mediums before deciding upon a hospital. This development has led to concerns regarding the insufficiency of medical resources in Korea (3).
Examining the matter of how to appropriately allocate the limited supply of medical resources is a crucial issue in terms of the management of a medical institution. In addition, we expect that developing and applying an efficient mathematical/economic model to management would contribute to making management more efficient. Given the importance of outpatients to medical institutions, the prediction of outpatient numbers has very practical and scientific implications. In this study, we employ daily data of hospitals specializing in the spine and joints to develop a prediction model of outpatient numbers, which we expect can be used as base material to inform near-term hospital management as well as the setting of policies.
Theoretical background
The ARIMA model (Auto Regressive Integrated Moving-Average)
The ARIMA model is a stochastic time series model that is widely employed in conducting research on demand prediction and other subjects and represents the most classical and general of all existing time series models. ARIMA model is a generalization of the ARMA model, which employs past observations and past errors to explain the current value of some time series. Whereas the ARMA model is only applicable to stationary series, the ARIMA model has the advantage of also being applicable to time series that exhibit somewhat non-stationary characteristics (4). And future predicted values are linearly related to various past observations as well as white noise (5). Thus, in this study, we have specified a time-series model that reflects the aforementioned features. For some ARIMA (p, d, g) model, p represents the order of the autoregressive model, d is the degree of differencing, and q is the order of the moving-average model. It has the following representation:
Here, ϕq (B) is the AR (autoregressive) model, B is the lag operator, d is the degree of differencing, Yt is the dependent variable (raw time series), δ is a constant, θq (B) is the MA (moving-average) model, and εt is white noise.
The ARIMA model has been widely used in social sciences for demand prediction and other purposes. However, when there are periodical elements present within a time series, the ARIMA model is limited in its ability to account for the effects of such periodicity. In cases where the data being examined exhibits seasonality or periodicity, applying the ARIMA model can be inadequate. The SARIMA model was developed to address this shortcoming of ARIMA models.
The SARIMA model (Seasonal Auto Regressive Integrated Moving Average)
Time series of various frequencies (quarterly, monthly, weekly, and daily) are referred to as being “seasonal” when they exhibit observable periodic trends due to seasonal variations. When working with such series, it is necessary to employ an ARIMA (p, d, q) (P,D,Q)S model, where p denotes the AR order and P denotes the seasonal AR order. In addition, d denotes the degree of difference and D denotes the degree of seasonal difference, while q and Q denote the MA order and seasonal MA order, respectively. The model can be expressed mathematically as follows:
Here, P denotes the order of seasonal AR terms, Q denotes the order of seasonal MA terms, and D denotes the degree of seasonal differencing. Eq. [2] is seen to be the same as Eq. [1], but augmented with the seasonal component, . As previously mentioned, prior to applying the Box-Jenkins methodology (ARIMA, SARIMA, etc.), it is necessary to ensure that the time series being modeled is stationary. In other words, the time series must be characterized as stationary, such that its features remain consistent regardless of the time, particularly in the future. As such, if a time series is assumed to be non-stationary, predictions derived from such data cannot be regarded as being stationary regardless of the model. Furthermore, the raw time-series data used in the model may also be insufficiently reliable for making predictions (6).
Literature review
Reviewing the previous literature reveals that various studies, both in Korea and overseas, have developed and analyzed predictive models based on outpatient data. Many studies estimated the number of outpatients based on weekly and monthly data from hospitals. While these studies developed the best-fitting models for predicting the number of outpatients by employing monthly and weekly data, the use of data with gaps in frequency has the disadvantage of being less than ideal for making near-term predictions (7-9). Thus, the use of such data may ultimately lead to an inability to strategically address managerial issues. Luo et al. [2017] employed daily outpatient data from a hospital in China to develop a predictive model of outpatient numbers over a one-year horizon (10). However, it was limited in that it did not take account of factors influencing the number of outpatients, such as the days of the week. In Korea, there have been almost no studies regarding predictive models for medical institutions. A study by Ji and Kim [2013], which employed ER center data to predict the demand for ER outpatient capacity, was the only Korean study of the kind we consider here (11).
Considering these issues comprehensively, we specified the time frequency of the model at the “daily” level as being appropriate for making accurate near-term predictions of outpatient numbers. The predictions derived from such data may be regarded as reflecting all realistic implications, including the overall administration of hospital management, response strategies, adjustments, and crisis indicators. In terms of periodic effects, because the frequency employed in this study is at the daily level, it would be appropriate to consider seasonal factors in addition to day-of-the-week variations. Thus, the present study developed a composite time series model that is used effectively in the field of predictive studies, including seasonal factors, SARIMA, and ARIMA. Furthermore, we compared the fitness of the two models to arrive at an optimal predictive model, thereby attempting to predict the number of outpatients more accurately.
The predictive model for outpatient numbers was specified based on the two aforementioned models. Estimation and analysis of these models were conducted using STATA 12.0.
Methods
This study employed outpatient data from January 1, 2014 to December 31, 2016 from “N” hospitals in Gangnam-gu, Seoul to develop a model for making predictions of the number of outpatients for the period from January 2, 2017 to December 31, 2017. The overall process is as described in Figure 1.
Model diagnostics and stationarity tests
As previously mentioned, stationarity tests were conducted to ensure that the time series to be analyzed is stationary prior to conducting modeling according to the Box-Jenkins methodology. Furthermore, because the time series being modeled here covers a year at the daily frequency, we also conducted a seasonal unit root test. This involved correlograms analysis and the augmented Dickey-Fuller (ADF) test to ensure the stationarity of the time series and to check for the presence of a seasonal unit root, respectively. Table 1 indicates that the autocorrelation coefficient starts off at a high value (0.0661) at lag length 1 and shows values close to zero at almost all other lag lengths.
Table 1
| LAG | AC | PAC | Q | Prob>Q | Autocorrelation | Partial autocorrelation |
|---|---|---|---|---|---|---|
| 1 | 0.0661 | 0.1343 | 1.0785 | 0.2990 | | | |- |
| 2 | −0.3164 | −0.7014 | 25.906 | 0.0000 | --| | -----| |
| 3 | −0.2007 | 0.0075 | 35.935 | 0.0000 | -| | | |
| 4 | −0.2202 | −0.0427 | 48.06 | 0.0000 | -| | | |
| 5 | −0.2545 | – | 64.322 | 0.0000 | --| | |
| 6 | 0.1406 | – | 69.309 | 0.0000 | |- | |
| 7 | 0.6674 | – | 182.11 | 0.0000 | |----- | |
| 8 | 0.1504 | – | 187.86 | 0.0000 | |- | |
| 9 | −0.2391 | – | 202.46 | 0.0000 | -| | |
| 10 | −0.2444 | – | 217.79 | 0.0000 | -| | |
| 11 | −0.2099 | – | 229.13 | 0.0000 | -| | |
| 12 | −0.2510 | – | 245.44 | 0.0000 | --| | |
| 13 | 0.1560 | – | 251.76 | 0.0000 | |- | |
| 14 | 0.6703 | – | 369.01 | 0.0000 | |----- | |
| 15 | 0.1370 | – | 373.93 | 0.0000 | |- |
LAG, time lags; AC, autocorrelation; PAC, partial autocorrelation; Q, Q-value.
The partial autocorrelation function measures the degree of correlation between two specific observations, Yt and Yt−K, while disregarding the influence of all other observations other than those at lag k. In other words, it indicates the net correlation between Yt and Yt−K after removing the effects of Yt−1, Yt−2, …, Yt−K+1. For some stationary time series {Yt}, the partial autocorrelation function of lag K represents the ê-th regression coefficient from the regression equation Yt=ϕK−1+ … + ϕKKYt−K + αt, and is expressed as the partial autocorrelation coefficient, ϕKK:
To identify the stochastic characteristics of an ARIMA model, it is necessary to calculate the mean, variance, and autocorrelation function of the series. Because the autocovariance varies depending on the measurement unit of the variable, in most cases the autocorrelation coefficient is calculated.
The autocorrelation function indicates the degree of interaction between observed values of the same variable at different points in time, thus measuring the degree of interaction between continued observations of the same variable. This can be expressed mathematically as follows:
Table 2 reports the results of the ADF test conducted on the raw time-series data. ADF testing was conducted for three scenarios: a random walk with no drift term, a random walk with a drift term, and a random walk with both a deterministic trend and a stochastic trend.
Table 2
| Scenarios | Tau value | P>|t| | Lags |
|---|---|---|---|
| Random walk | −5.218 | 0.001 | 3 |
| Random walk with drift | −5.209 | 0.001 | 3 |
| Random walk with drift and trend | −5.365 | 0.001 | 3 |
ADF, augmented Dickey-Fuller.
Based on the results of the ADF tests in Table 2, we can reject the null hypothesis that the tested time series “has a unit root,” or equivalently, “is non-stationary” at the 1% significance level. That is, we may regard the time series as stationary. Via this process, the optimal models that were employed in this study were determined to be ARIMA (3,0,2) and SARIMA (2,0,1) (1,0,0)6.
Model selection theory
White test
Due to the random error term in the model, the presence of heterogeneity will adversely affect the prediction accuracy of the model. To select a model that is free of heterogeneity, we employed the White test. This test performs a test for heterogeneity based on a chi-square statistic derived from an auxiliary regression. If a model with a random error term is able to reject the null hypothesis of the test, heterogeneity is not present. On the other hand, if one is unable to support the alternative hypothesis, there is heterogeneity in the model, and this may affect the predictions made by it.
2, which takes a value between 0 and 1, is an important indicator of a regression model’s goodness of fit. The closer this value is to 1, the better fit the model is considered to have. However, using R2 as the criterion for model selection has the possible disadvantage of resulting in a loss of degrees of freedom in the prediction model. This is because, unlike regressions in general, prediction models must account for the fact that it is impossible to simply add variables based on increments of 2. In view of this, we used the adjusted value of 2 for model selection purposes. This indicator can be expressed mathematically as follows:
Here, n is the sample size and k is the number of explanatory variables. The use such adjusted indicators has the advantage of circumventing the influence of events occurring at certain time points.
AIC, BIC, and SC
When estimating models, indicators such as the AIC (Akaike information criterion), SC (Schwarz criterion), and BIC (Bayesian information criterion) change depending on the lag length. In selecting the lag length of our model, we aim to choose that which has smaller values of these indicators, while also taking the results of the significance tests for each term’s parameters as well as model parsimony into consideration. Model selection was based on models with higher values of 2 and smaller values of AIC, BIC, and SC.
Because model identification is not straightforward in mixed models such as SARIMA, AIC and BIC are employed to address this issue. Using the two information criterions, we select the model with the lowest AIC value.
Here, n is the number of time series observations, is the maximum likelihood estimator of , and (p+q) is the number of parameters in the specified model.
Results
Model estimation results
Based on the aforementioned model, the results of the inference on outpatient numbers are as follows.
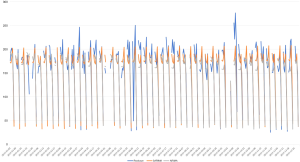
Figure 2 indicates that the results from the SARIMA model are relatively closer to the actual values compared to those of the ARIMA model. However, the regression results of each model must be examined for more precise analysis. The results of this analysis are as follows (Table 3).
Table 3
| ARIMA (3,0,2) | SARIMA (2,0,1) (1,0,0)6 | ||||
|---|---|---|---|---|---|
| Coef (Std, Err) | Z-value (P>|z|) | Coef (Std, Err) | Z-value (P>|z|) | ||
| AR | |||||
| AR [1] | 0.603 (0.273) | 2.21 (0.027) | 0.921 (0.105) | 8.78 (0.001) | |
| AR [2] | −0.146 (0.262) | −0.56 (0.577) | −0.004 (0.065) | −0.06 (0.951) | |
| AR [3] | 0.281 (0.068) | 4.12 (0.001) | – | – | |
| MA | |||||
| MA [1] | −0.402 (0.285) | −1.41 (0.158) | −0.062 (0.068) | −0.90 (0.367) | |
| MA [2] | 0.043 (0.225) | 0.18 (0.853) | – | – | |
| Constant | 44.773 (8.074) | 5.55 (0.001) | 44.15 (8.19) | 5.39 (0.001) | |
| AIC | 13.8954 | 13.1512 | |||
| BIC | 14.9871 | 13.9984 | |||
AR, auto regressive; MA, moving average; AIC, Akaike information criterion; BIC, Bayesian information criterion.
In the cases of the ARIMA (3,0,2) and SARIMA (2,0,1) (1,0,0)6 models, which were deemed to be the ex-ante optimal models, z-test results revealed that the AR terms were mostly significant. However, the AR terms of the ARIMA (3,0,2) model were not found to be significant. Furthermore, comparisons of the AIC and BIC values for model evaluation showed that the SARIMA (2,0,1) (1,0,0)6 model had smaller values. As smaller values of the AIC and BIC are indicative of better fit, we regard the predicted values from the SARIMA (2,0,1) (1,0,0)6 model to be more accurate than those from the ARIMA (3,0,2) model.
Model test results
Table 4 summarizes the various basic statistical indicators of the two models described above. In terms of the heteroskedasticity test, both models passed the White test at the 1% significance level. This can be interpreted as indicating that the variance of the error terms in the models exhibit no difference. In terms of goodness of fit, the SARIMA model had a greater 2 value than the ARIMA model with the seasonal factor. Thus, the former was deemed to have better fit. As previously mentioned, the SARIMA model had smaller values of AIC and BIC, thus indicating better fit.
Table 4
| Model | ARIMA | SARIMA |
|---|---|---|
| White test | 0.0135 | 0.0001 |
| 2 | 0.4241 | 0.4553 |
| AIC | 13.8954 | 13.1512 |
| BIC | 14.9871 | 13.9984 |
AIC, Akaike information criterion; BIC, Bayesian information criterion.
Table 5 reports the prediction performance of the two models. Compared side by side, the SARIMA model had smaller values in all error indicators than the ARIMA model. In terms of the seasonal factors, it was also clearly apparent that the predicted values of the SARIMA model could be closer to the actual values. Meanwhile, looking at the correlation coefficient between the model values and the actual values, that of the SARIMA model SARIMA (0.8992) was greater than that of the ARIMA model with the seasonal factor (0.8486). That is, this may be regarded as a supplementary indicator of the SARIMA model’s better fit.
Table 5
| Days | ARIMA | SARIMA |
|---|---|---|
| MSE | 162.65 | 160.21 |
| MAPE | 10.897% | 9.812% |
| RMSE | 7.919 | 7.424 |
| Correlation Coef. | 0.8484 | 0.8992 |
Discussion
In keeping with this trend, this study developed a prediction model of the number of outpatients at hospitals specializing in the spine and joints using daily data compiled from basic patient data. Rather than being simply a model for predicting profits at hospitals, we believe that the model developed herein will provide theoretical support for the reallocation of medical personnel and enable adequate preparations for emergency situations through accurate predictions.
The ARIMA model has been widely employed in time-series modeling and has been recognized for its reliability and accuracy in the field of forecasting. We believe that the application of the SARIMA model, which augments ARIMA with seasonal effects, has provided high-quality base materials for the study of the number of outpatients at hospitals specializing in the spine and joints. The performance of the models was evaluated, and conclusions were derived based on comparisons of experimental results and actual data. As a result, we found that the SARIMA model outperformed competing models by a considerable margin, suggesting that it will serve as a suitable model for predicting the number of outpatients at hospitals specializing in the spine and joints in the future.
One of the most important things in choosing a model is to choose the appropriate way to make the best trade-off between compliance and the complexity of modeling (number of variables). In this paper, we select ARIMA and SARIMA and models to capture seasonal patterns, describe the characteristics of self-correlation, propensity and cyclicality as well as the daily effects from different sub-time series data, and set up a linear coupling model based on the above model with residual revision approval. Both models have good performance in predicting accuracy. However, the ARIMA model had a MAAPE value of 0.1090 and 0.098 for the SARIMA model. In this study, the combination model is superior in modifying the extreme values of daily outpatient volume over the SARIMA model, especially for the value of weekend data. The findings are similar to those analyzed by Luo et al. [2017] (10).
Conclusions
In the present era, medicine continues to be a central aspect of our lives. In November 2018, president Moon Jae-in’s administration introduced a policy of deregulation regarding medical big data for the activation of the data economy. Thus, as the outlook for related industries is expected to grow in importance, the analysis of primary data, that is, patient data, is expected to become more important in the future.
Based on the findings of this study, such hospitals will be able to develop predictive models that will aid in the future allocation of personnel while also guaranteeing the monitoring of illnesses in real time. However, one limitation of this study is that it did not consider exogenous variables that may influence the number of outpatients, such as the weather or changes in policy. We expect that future research will address these shortcomings, thereby developing more accurate and reliable predictive models that will enable the provision of higher-quality service by medical institutions.
Acknowledgments
Funding: None.
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/jhmhp-20-29). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Lee J. Population aging and economic growth: Impact and policy implications. KDI Policy Forum. 2019:273.
- Oh YH. The policy direction and tasks of master plan for health examination in Korea. Healthcare forum 2004;3:51-61.
- Park BS, Lee YG, Kim YS. Efficiency evaluation of general hospitals using DEA. The Korea Contents Society 2009;9:299-312. [Crossref]
- Box GEP, Jenkins GM. Time series analysis: Forecasting and control. J Am Stat Assoc 1970;68:199-201.
- Box GEP, Jenkins, GM, Reinsel GC. Time-series analysis, forecasting and control. San Francisco; Holden Day, 2013.
- Wooldridge JM. Introductory econometrics: A modern approach. 6th ed., Cengage, 2016.
- Cheng CH, Wang JW, Li CH. Forecasting the number of outpatient visits using a new fuzzy time series based on weighted-transitional matrix. Expert Syst Appl 2008;34:2568-75. [Crossref]
- Jiang S, Chin KS, Wang L. Modified Genetic Algorithm-based Feature Selection Combined with Pre-trained Deep Neural Network for Demand Forecasting in Outpatient Department. Expert Syst Appl 2017;82:216-30. [Crossref]
- Bergs J, Heerinckx P, Verelst S. Knowing what to expect, forecasting monthly emergency department visits: A time-series analysis. Int Emerg Nurs 2014;22:112-5. [Crossref] [PubMed]
- Luo L, Luo L, Zhang X, et al. Hospital daily outpatient visits forecasting using a combinatorial model based on ARIMA and SES models. BMC Health Serv Res 2017;17:469. [Crossref] [PubMed]
- Ji HN, Kim MS. Forecasting the Demand for Hospital Patients Using the Hourly Data of the Emergency Medical Center. Korea Intelligent Information Systems Society 2013;6:261-4.
Cite this article as: Kim KR, Park JE, Jang IT. Outpatient forecasting model in spine hospital using ARIMA and SARIMA methods. J Hosp Manag Health Policy 2020;4:20.